训练时的显存开销

原文来自我的飞书：https://et1q7qdh0g.feishu.cn/wiki/HSquw0zPZiJlM5kzm5xcVAv4nbg?from=from_copylink

训练时的显存开销都有哪些？

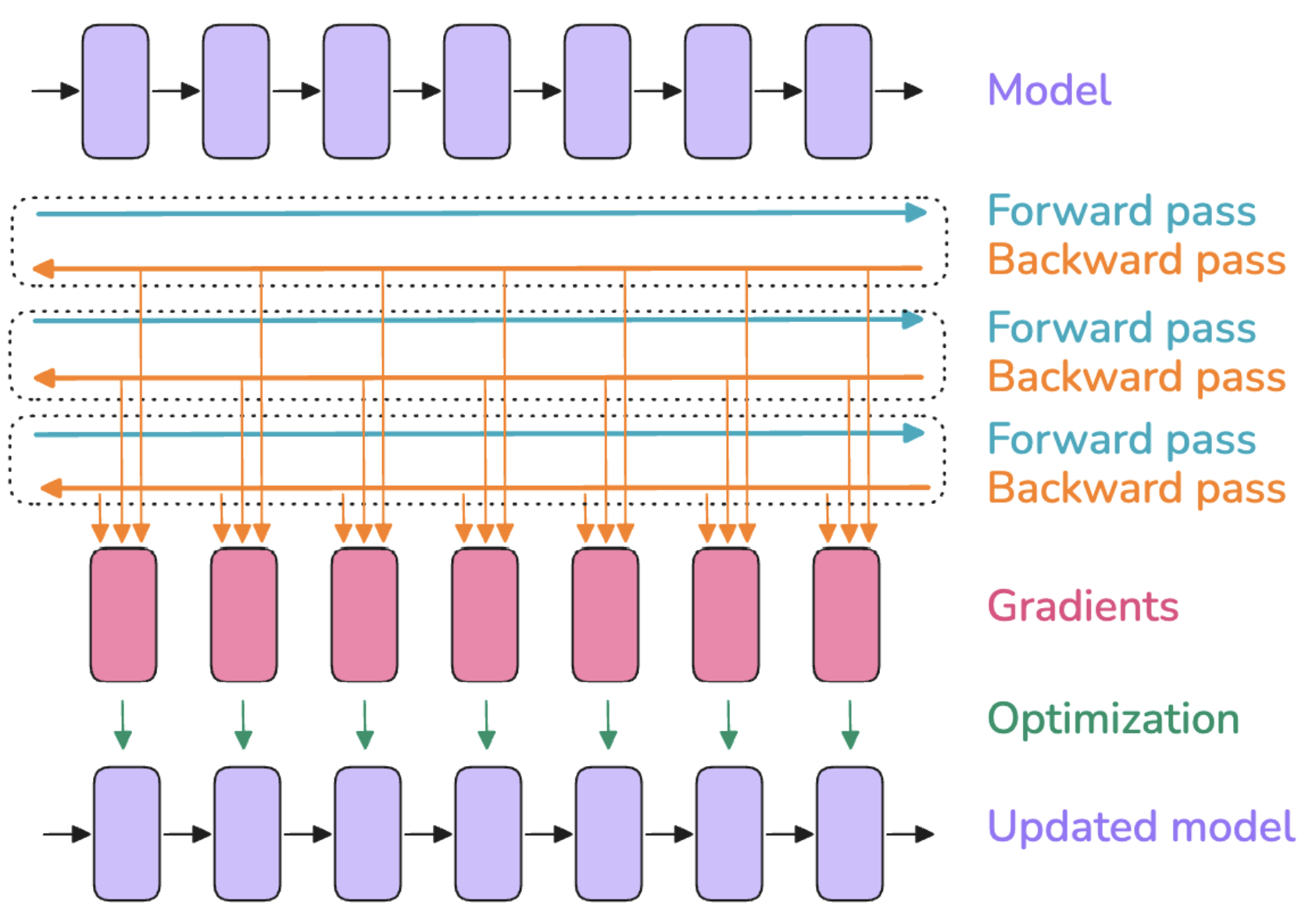
首先来复习一下模型在训练时的流程：

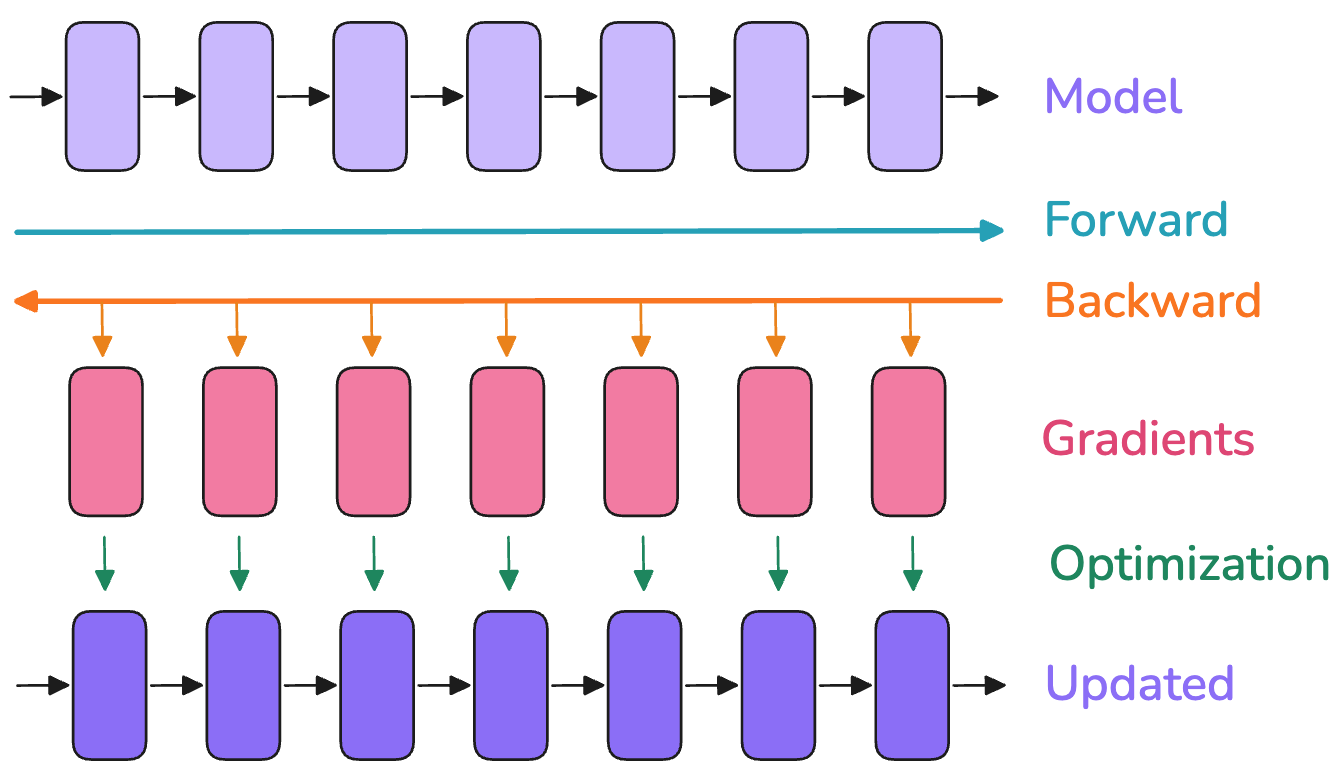
（图片来源：https://huggingface.co/spaces/nanotron/ultrascale-playbook?section=first_steps:_training_on_one_gpu）

1. 前向传播：模型接受输入，经过中间各个层得到激活值（activations），最后得到输出

2. 反向传播：通过最终的输出，进行反向传播算出来梯度

3. 优化器更新：所有梯度计算完之后，优化器使用这些计算出来的梯度来更新模型参数

所以模型在训练时的显存占用主要来源于以下四个部分：

1. 模型参数：由模型结构决定，在整个训练周期的显存占用不变

2. 模型梯度：在反向传播时逐渐增加，在优化器更新后释放，峰值大小和参数量相同

3. 优化器状态：比如目前最常用的 AdamW，需要存储梯度的一阶矩和二阶矩，是参数量的两倍

4. 激活值：由输入大小决定（batch_size x sequence_length），随着前向传播的进行不断增长，随着反向传播的进行不断减少

显存开销随时间如何变化？

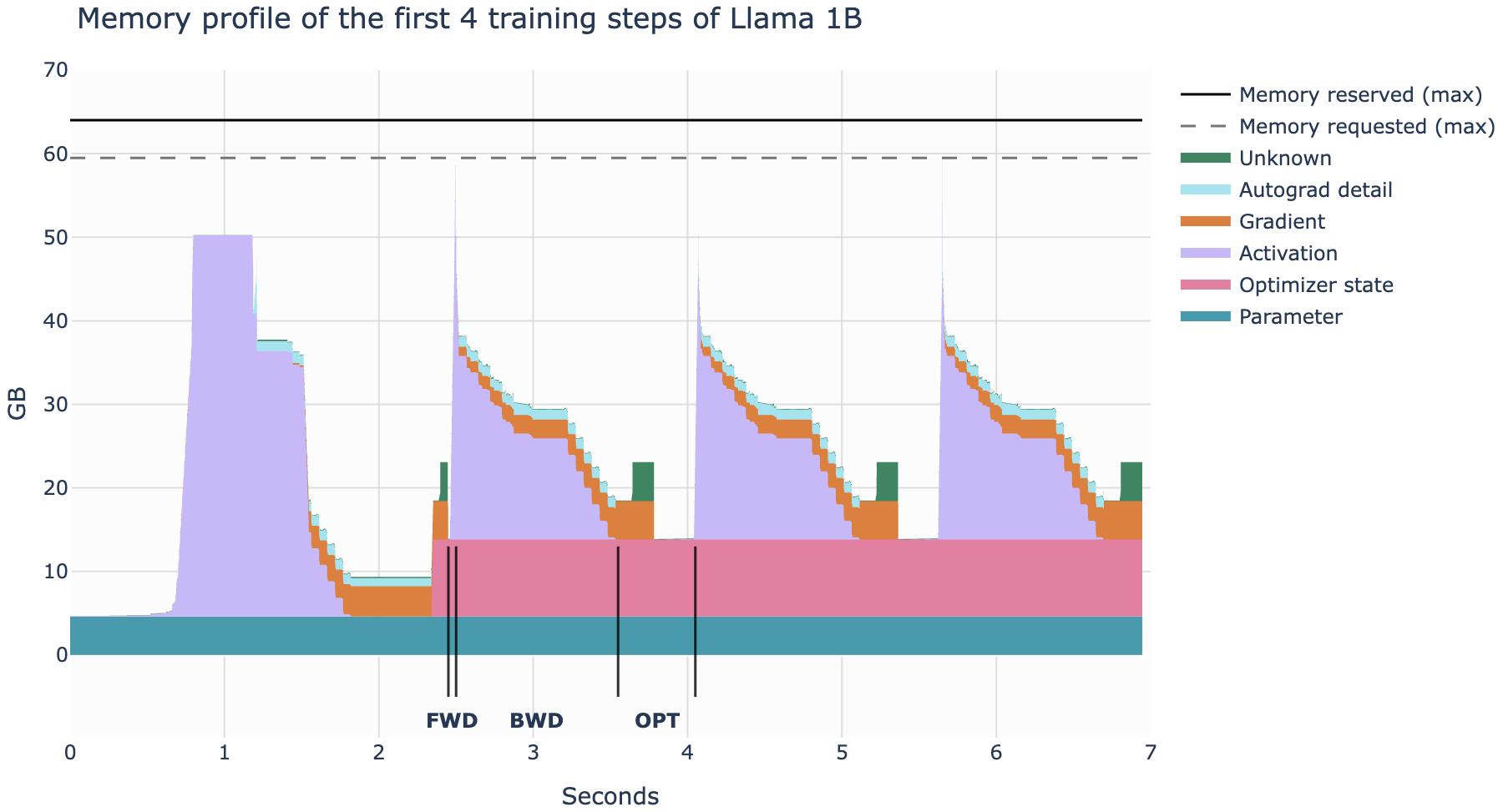
上图展示了用 pytorch profiler 抓取的 llama 1B 训练时的显存占用情况。

最底层是模型参数本身，从最开始到结束一直占用固定的显存量。（4.6GB）

从接近 3 秒开始的倒数第二层是优化器状态，一直到结束同样也是占用固定的显存量（大小为模型参数的两倍），前两秒之所以还没有优化器状态的显存占用，是因为第一次前向传播反向传播后，在执行 optimizer.step() 时才为优化器状态分配内存。（9.2GB）

从图中可以看到，前向的过程比反向过程快的多，第一次前向完成后会有一小段保持的时间，此处是 pytorch 的 cache allocator 在准备一些内存分配以加快后续的执行流程。

激活值（峰值占用 45.4GB）在前向的时候快速增长，在反向传播的时候缓慢阶梯式下降，梯度的占用则在反向传播的时候逐步上升，最后根据梯度来更新优化器状态。

此外还有一些其他的显存开销，比如 CUDA kernel 启动的时候需要大概 1-2GB 的显存，还有一些中间计算会占用一些显存，还有一些显存因为碎片问题是用不到的。

如何推导训练时的显存开销？

首先看前三个部分，也就是模型参数、梯度、优化器状态，这三个部分占用的显存大小只和模型本身有关（和模型的输入无关），假如我们计算出来模型参数量为 \(N\)，那么梯度的数量同样也是 \(N\)，优化器状态考虑最常用的 AdamW 的话则是 \(2N\)，然后我们在根据参数、梯度、优化器状态的实际精度（比如是 FP32 还是 BF16 还是 FP8 等等），计算出来对应的字节数即可。

所以现在我们先看如何计算模型参数量 \(N\)。

模型参数量：对于一个简单的 Transformer LLM 来说，其模型参数量可以通过以下公式进行计算：

\[\begin{align} N = h\cdot v + L(12 h^2+13 h)+2h \end{align}\]

其中 \(h\) 表示隐藏层大小，\(v\) 表示字符集大小，\(L\) 表示有多少层（Decoder Layer），这个公式基本按照 GPT2 来的，里面做了一些假设和简化：

• 存在 weight tying：输入 embedding 层和输出层共享权重，对应 \(h\cdot v\)，并且不考虑带参数的位置编码，GPT2 本身的位置编码是加相同的参数量学出来的，现在一般都是不含参数的 RoPE，因此这部分计算成 \(h\cdot v\) 而不是 \(2h\cdot v\)

• 每一个 Decoder Layer 内部的线性层都是带了 bias 的，因此 Attention 部分一个映射 \(q\) 的线性层的参数就是 \(h^2+h\)，那么映射 \(q,k,v,o\) 的总参数就是 \(4(h^2+h)=4h^2+4h\)，然后再考虑 MLP 部分，这里假设 MLP 中间升维后是 \(4h\)（也就是四倍，GPT2 是四倍，其他开源模型不一定是整四倍，这里做假设估算，按四倍来），那么 MLP 部分的参数就是 \((4h^2+4h)+(4h^2+h)=8h^2+5h\)，再考虑两个 Pre-LayerNorm，每个 Pre-LayerNorm 需要为每个参数保存两个值（scale \(\gamma\) 和 bias \(\beta\)），也就是 \(4h\)，那么总计就是 \(12h^2+13h\)

• 在最后一个 Decoder Layer 后面还有一个 LayerNorm，对应 \(2h\)

画个图：

+------------------------------------------------------+
| Input Embeddings (h·v parameters)                    |
+------------------------------------------------------+
+------------------------------------------------------+
|                  DECODER LAYER 1..L                  |
| +--------------------------------------------------+ |
| | Self-Attention Block                             | |
| | +-----------------+  +-----------------+         | |
| | | Pre-LayerNorm   |  | Linear Layers   |         | |
| | | (2h parameters) |  | Q,K,V,O         |         | |
| | |                 |  | (4h²+4h params) | Total:  | |
| | +-----------------+  +-----------------+ 4h²+6h  | |
| +--------------------------------------------------+ |
| +--------------------------------------------------+ |
| | MLP Block                                        | |
| | +-----------------+  +-----------------+         | |
| | | Pre-LayerNorm   |  | Linear Layers   |         | |
| | | (2h parameters) |  | Up & Down       |         | |
| | |                 |  | (8h²+5h params) | Total:  | |
| | +-----------------+  +-----------------+ 8h²+7h  | |
| +--------------------------------------------------+ |
| Total: 12h² + 13h parameters per layer  (times L)    |
+------------------------------------------------------+
+------------------------------------------------------+
| Final LayerNorm (2h parameters)                      |
+------------------------------------------------------+
+------------------------------------------------------+
| Output Projection (weight tied to Input Embeddings)  |
| (No additional parameters due to weight tying)       |
+------------------------------------------------------+

可以再看一下 Self-Attention Block 的参数计算细节：

+------------------------------------------+
| Pre-LayerNorm                            |
| - Gamma (scale): h parameters            |
| - Beta (bias): h parameters              |
| TOTAL: 2h parameters                     |
+------------------------------------------+
                     SPLIT          
+-------------+  +-------------+  +-------------+
| Q Projection|  | K Projection|  | V Projection|
| - Weights:  |  | - Weights:  |  | - Weights:  |
|   h × h = h²|  |   h × h = h²|  |   h × h = h²|
| - Bias: h   |  | - Bias: h   |  | - Bias: h   |
| TOTAL: h²+h |  | TOTAL: h²+h |  | TOTAL: h²+h |
+-------------+  +-------------+  +-------------+
+------------------------------------------+
| Attention Computation                    |
| - Matrix multiplications                 |
| - Softmax                                |
| (No learnable parameters)                |
+------------------------------------------+
+------------------------------------------+
| Output Projection                        |
| - Weights: h × h = h²                    |
| - Bias: h                                |
| TOTAL: h²+h parameters                   |
+------------------------------------------+
TOTAL PARAMETERS: 2h + 3(h²+h) + (h²+h) 
                  = 4h² + 6h

然后再看一下 MLP 的参数计算细节：

+------------------------------------------+
| Pre-LayerNorm                            |
| - Gamma (scale): h parameters            |
| - Beta (bias): h parameters              |
| TOTAL: 2h parameters                     |
+------------------------------------------+
+------------------------------------------+
| Up Projection (Expansion)                |
| - Input size: h                          |
| - Output size: 4h (4× expansion ratio)   |
| - Weights: h × 4h = 4h²                  |
| - Bias: 4h                               |
| TOTAL: 4h² + 4h parameters               |
+------------------------------------------+
+------------------------------------------+
| Activation Function (GELU/ReLU/etc.)     |
| (No learnable parameters)                |
+------------------------------------------+
+------------------------------------------+
| Down Projection (Compression)            |
| - Input size: 4h                         |
| - Output size: h                         |
| - Weights: 4h × h = 4h²                  |
| - Bias: h                                |
| TOTAL: 4h² + h parameters                |
+------------------------------------------+
TOTAL PARAMETERS: 2h + (4h² + 4h) + (4h² + h)
                  = 8h² + 7h

这里我们其实可以观察到，由于 MLP 里面有个升维操作，每一层对应的参数量是 \(8h^2\)这个级别，而 Attention 部分对应的参数量是 \(4h^2\) 这个部分，也就是说 MLP 部分的参数大概是 Attention 部分的两倍，对于总模型参数量来说，可以大概认为 MLP 占了总模型参数量的 \(\frac{2}{3}\)，Attention 占了总模型参数量的 \(\frac{1}{3}\)。

好，你记住了吗？\(N = h\cdot v + L(12 h^2+13 h)+2h\)？但是实际上大部分时候不需要我们自己去计算模型参数量，因为我们使用的时候，参数量自己是会在名字里的，比如 Llama-2-7B，他就是个 7B 参数量的模型。不过这个公式的好处是可以做一些估算，比如我们可以近似为 \(N\approx 12L\cdot h^2\)，这样我们只需要知道模型的层数和隐藏层大小（通常也被成为 Model Dimension），做快速的参数估算。

此处还要注意较新的模型可能会用 RMS-Norm，此时就就会只有 \(h\) 个参数而非 LayerNorm 的 \(2h\)

并且线性层有的模型是不加 bias 的，这部分参数量也会减少

现在我们知道了模型参数量为 \(N\) 之后，我们怎么计算我们训练这个模型需要多少显存？

首先简单一点，我们对参数、梯度、优化器状态都采用单精度浮点数计算，也就是 FP32，每个 FP32 是 4 个字节，因此：

• 模型参数消耗的显存是 \(4N\)

• 模型梯度消耗的显存是 \(4N\)

• 优化器状态消耗的显存是 \(8N\)

总计 \(16N\)。

这里优化器按之前的假设为 AdamW，会为每个参数的梯度存储他的一阶矩和二阶矩，所以是两倍的显存开销。

而当前更加常见的训练方式实际上是混合精度训练（Mixed Precision Training）：

• 模型参数使用 BF16：消耗显存 \(2N\)

• 模型梯度使用 BF16：消耗显存 \(2N\)

• 模型参数的 FP32 副本：消耗显存 \(4N\)

• 优化器状态为了保证数值稳定性仍然使用 FP32：消耗显存 \(8N\)

总计 \(16N\)。

我们发现好像混合精度训练之后，显存占用量是不变的，其中模型参数还要额外保存 FP32 的副本，并且优化器状态的数值精度也完全不变，这一切都是为了保证数值计算的稳定性，相当于只有在前向传播和反向计算梯度的时候使用 BF16，在用梯度更新模型参数以及优化器状态时需要在 FP32 的精度下执行。

一些实现为了避免 BF16 的数值不稳定性，甚至还会额外存一份 FP32 的梯度，导致混合精度训练可能还会有额外的 \(4N\) 的显存开销，得到总计 \(20N\) 的显存占用量

那么混合精度训练看上去没有降低显存？他确实没有降低模型参数+梯度+优化器状态的显存，但是他可以降低激活值所占据的显存，并且 BF16 在 GPU 上有更高的 FLOPS，可以加速训练。

所以当我们拿到一个参数量为 \(x\)B 的模型之后，可以得知他的模型参数+梯度+优化器状态就需要 \(16x\) GB 的显存。

比如我们训练一个 7B 的模型，他的参数+梯度+优化器状态就需要 \(7\times 16=112\) GB 的显存，加上激活值则会更多，这已经超过了单张 GPU 的显存大小（比如 H100 的显存大小是 80GB）。

现在先不考虑多 GPU 情况，仍然考虑模型在一张 GPU 里进行训练，我们还剩激活值没有讨论。

根据 NVIDIA 的 paper Reducing Activation Recomputation in Large Transformer Models，激活值所需要的显存为以下字节数（前向传播过程中按 BF16 来计算，每个元素占两个字节）：

\[\begin{align} L\cdot seq\cdot bs\cdot h\cdot(34+\frac{5n_{heads}\cdot seq}{h}) \end{align}\]

其中 \(L\) 为层数，\(seq\) 为序列长度（简写为 \(s\)），\(bs\) 为批大小（简写为 \(b\)），\(h\) 为隐藏层大小，\(n_{heads}\) 为 Attention 的头数（简写为 \(a\)）。

哪些激活值要保存下来？其实不是所有的激活值都要保存下来，而是只有被反向传播使用到的激活值才需要保存下来，举两个例子：

第一个例子是普通的线性层 \(y=xW\)，其中 \(W\) 是参数矩阵，需要梯度，而计算其梯度为 \(\frac{\partial L}{\partial W}=(\frac{\partial L}{\partial y})^\top \frac{\partial y}{\partial W}=(\frac{\partial L}{\partial y})^\top x\)，其中 \(\frac{\partial L}{\partial y}\) 是 Loss \(L\) 相对于 \(y\) 的梯度（代码里面一般写作 out_grad），这里使用了一个链式法则，然后有一些矩阵转置是为了符合矩阵乘法的维度的（为了严谨一点），不过可以大致理解这个意思，反正我们最后看到就是说，这个需要计算 \(W\) 的梯度的话，就需要保存 \(x\) 这个激活值。

第二个则是普通的残差连接中的小加法 \(z=x+y\)，其中 \(x,y\) 也都需要梯度，同样我们计算 \(\frac{\partial L}{\partial x}=\frac{\partial L}{\partial z}\frac{\partial z}{\partial x}=\frac{\partial L}{\partial x}\)，也就是说这个残差连接实际上就是把要回传的梯度复制了两份给到两个输入分支上，因此不需要保存这两个激活值 \(x,y\)，当然，对于残差连接这个算子不需要保存，假如 \(x,y\) 同时又参与到其他算子的计算，根据算子的不同梯度计算方式，\(x,y\) 可能就需要保存了。

因此我们在分析哪些激活值要保存时，一定要按照算子来进行分析，分析算子的哪些输入需要保留，大家去读一下 Reducing Activation Recomputation in Large Transformer Models 的 4.1 小节，就会发现作者正是这样分析的。

下面我们来详细推导哪些激活值需要保存，依次看 Attention 模块和 MLP 模块，此处的模型结构一些细节会和上一部分的不太一样，主要是为了和 paper 中的图与数据进行对齐。此处我们假设 Attention 模块的 Softmax 后有 Dropout 层，并且 Attention 模块的最后输出后面也有一个 Dropout 层。

以下进行详细分析：

Attention 模块：

• 输入会走到一个大的线性层，线性层的输出分成三份得到 \(Q,K,V\)，从之前的第一个例子我们可以知道，线性层的所有输入激活值都是需要保存的，因此此处保存输入激活值，其大小为：\(\color{red}{2sbh}\) （注意这里已经都是字节数，所以乘了 \(2\)）

• 接下来我们看 \(QK^\top\) 矩阵乘法，其后面的梯度要往前传播的话，这里类似线性层的乘法，因此两个输入激活值都要保存，\(Q,K\) 一块保存的显存大小是 \(\color{red}{4sbh}\)

• 然后看 Softmax 运算，这一块可以推一下他的导数（此处略去），可以发现回传梯度的话同样是需要他的所有输入的，因此 Softmax 的输入 \(QK^\top\) 需要保存下来，对应的显存大小是 \(\color{red}{2as^2b}\)

• 如前所述，我们假设 Softmax 后面有一个 Dropout，他的操作实际上是 \(y=\text{dropout}(x)=\frac{\text{mask}\odot x}{1-p}\)，其中 \(p\) 是 dropout 的概率，\(\text{mask}\) 则是此次被 dropout 的元素位置信息掩膜，这里面 \(\text{mask}, p\) 这些都是不需要梯度的，只有 \(x\) 需要梯度，而他的梯度是 \(\frac{\partial L}{\partial x}=\frac{\text{mask}}{1-p}\odot \frac{\partial L}{\partial y}\)，此处我们发现计算 \(x\) 的梯度是不需要 \(x\)的，因此 Dropout 的输入激活值不需要被保存，但是 Dropout 本身这个 \(\text{mask}\) 是需要保存的，对于他来说我们认为每个位置占用一个字节，因此对应的显存大小是 \(\color{red}{as^2b}\)

• Softmax + Dropout 后得到的就是 attention score 了，这个 score 需要乘上 \(V\) 得到 \(O\)，显然乘法操作需要保存所有的输入激活值以便回传梯度，因此 score 和 \(V\) 都要保存，分别对应显存大小为 \(\color{red}{2as^2b}\) 和 \(\color{red}{2sbh}\)

• 接下来 \(O\) 又会经过另一个线性层，对于线性层，我们需要保存其输入以回传梯度，也就是 \(O\) 要保存，对应显存大小 \(\color{red}{2sbh}\)

• 如前所说，我们在最后还会加一个 Dropout，而 Dropout 不需要保存其输入，但是需要保存 \(\text{mask}\)，也就是 \(\color{red}{sbh}\)

把这些值加起来，就可以得到 Attention 模块总共需要显存量

\[\begin{align} 2sbh+4sbh+2as^2b+as^2b+2as^2b+2sbh+2sbh+sbh=\color{blue}{11sbh+5as^2b} \end{align}\]

MLP 模块：

• 首先是一个线性层做升维，把 \(h\) 升到 \(4h\)（假设是四倍），之前我们知道，线性层要保存输入激活值，此时的输入激活值显存大小是 \(\color{red}{2sbh}\)

• 然后经过一个非线性激活函数，比如 ReLU，GeLU 啥的，这里就比较微妙了，假如用的是 ReLU 的话，实际上其正象限对应的导数是 \(1\)，负象限则是 \(0\)，就和输入 \(x\) 没啥关系了，不用存输入激活值，但是我们这里按照 paper 里的假设来，认为他是 GeLU（Gaussian Error Linear Units），\(\text{GeLU}(x)=x\cdot \Phi(x)\)，其中 \(\Phi(x)\) 为标准正态分布的累积分布函数，他的导数是这个样子 \(x\cdot\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}+\Phi(x)\)，明显是和 \(x\) 相关的，因此这个输入激活值需要保存，对应显存大小为 \(\color{red}{8sbh}\)

• 然后再经过一个线性层做降为，同样保存激活值，显存大小为 \(\color{red}{8sbh}\)

• 最后再经过一个 Dropout，保存他的 \(\text{mask}\)，显存大小为 \(\color{red}{sbh}\)

把这些值加起来，就可以得到 MLP 模块总共需要显存量 \(\begin{align} 2sbh+8sbh+8sbh+sbh=\color{blue}{19sbh} \end{align}\)

最后别忘了 Attention 模块和 MLP 模块前面各自都有一个 PreNorm Layer，需要保存他们的输入攻击\(\color{blue}{4sbh}\)（计算时忽略掉保存的均值和方差）

是不是还有每个模块后面的残差连接？是否需要额外再保存什么激活值？比如 Attention 和 MLP 模块最后 Dropout 的输出是否有可能需要保存？正如之前分析，残差连接本质是个加法，直接把输出的梯度送给两个输入就行了，不需要通过输入本身来计算梯度，所以不需要保存额外的激活值

至此，我们可以得到一个 Decoder Layer 所需要的显存大小为：

\[\begin{align} (11sbh+5as^2b)+19sbh+4sbh=\color{purple}{sbh(34+5\frac{as}{h})} \end{align}\]

也就是我们一开始给的公式。

从公式中我们可以观察出来什么？激活值所需要的显存随着 batch size （\(b\)）的增加是线性增长的，但是随着序列长度（\(s\)）的增加是二次方增长的，有个很好的图：

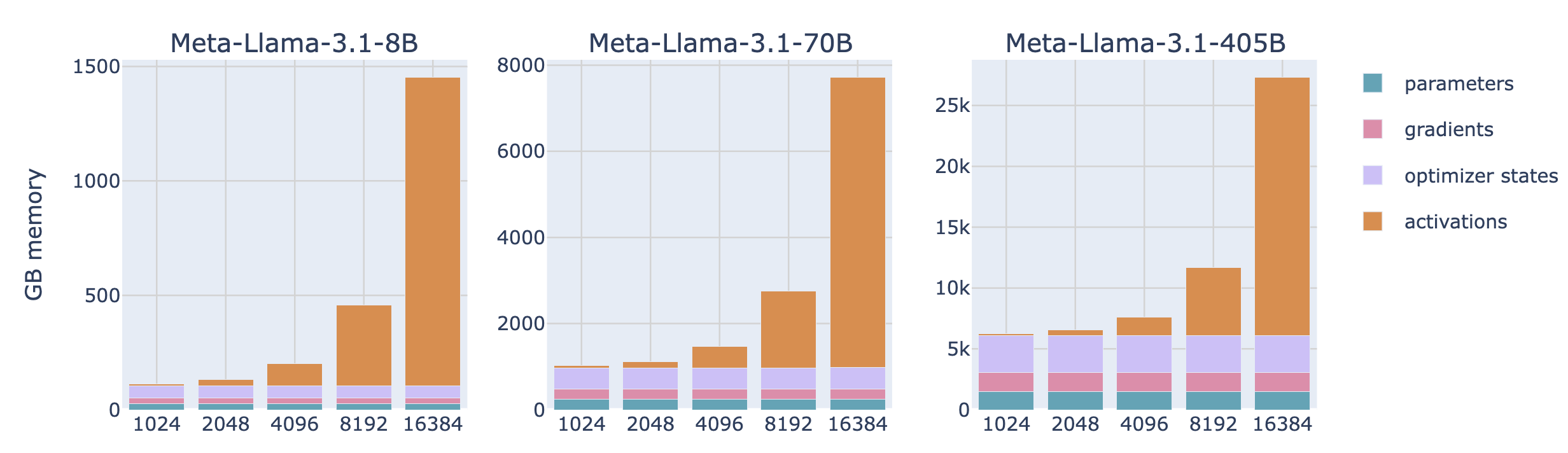
（图片来自 https://nanotron-ultrascale-playbook.static.hf.space/dist/index.html?section=first_steps%3A_training_on_one_gpu#activations_memory）

从图中可以看出，当序列长度小于 4k 的时候，基本上还是模型参数、梯度、优化器状态占据显存的主导地位，但是当序列长度不断增长，激活值所占据的显存会远远超过模型本身。

为了应对激活值显存占用过大，主要有两个方法：

1. Activation recomputation（激活值重计算）：也称为 gradient checkpointing（梯度检查点）或 rematerialization，实际上就是只在部分地方保存激活值，在梯度反向传播需要特定的未保存的激活值时，从前一个保存的激活值重新进行以下前向传播，这一部分可以直接把 Attention 相关的激活值都干掉，从而干掉总显存里面的那个 \(s^2\) 项，使得显存占用不随着序列长度的增长而二次方增长，并且目前最流行的 FlashAttention 的实现已经默认内置了 Attention 激活值重计算，可以大幅减少显存占用，虽然看上去重新计算有额外的计算开销，但是实际上如果激活值都存下来的话，反而需要从显存中进行读取，会有访存的开销。

2. Gradient accumulation（梯度累积）：实际上应对的是显存占用随着 batch size 的增长而线性增长的问题。操作就是把 batch size 拆成 gradient accumulation step 个 micro batch size，这样每次只过一个 micro batch size 的数据，减少了显存的占用，每次过完一个 micro batch size 的数据之后并不立即更新模型参数，而是在梯度上做累积，直到过了 gradient accumulation step 次之后，再取平均的梯度值对模型参数进行更新，这样就又能享受到大的 batch size 带来的好处。这时一般会把 batch size 叫做 global batch size，并且我们会发现 micro batch 之间其实是可以独立并行的，这里自然会想到用多个 GPU，每个 GPU 处理不同的 micro batch size，从而引入数据并行的相关设计。

这两种方法的图片可以参考：

激活值重计算：

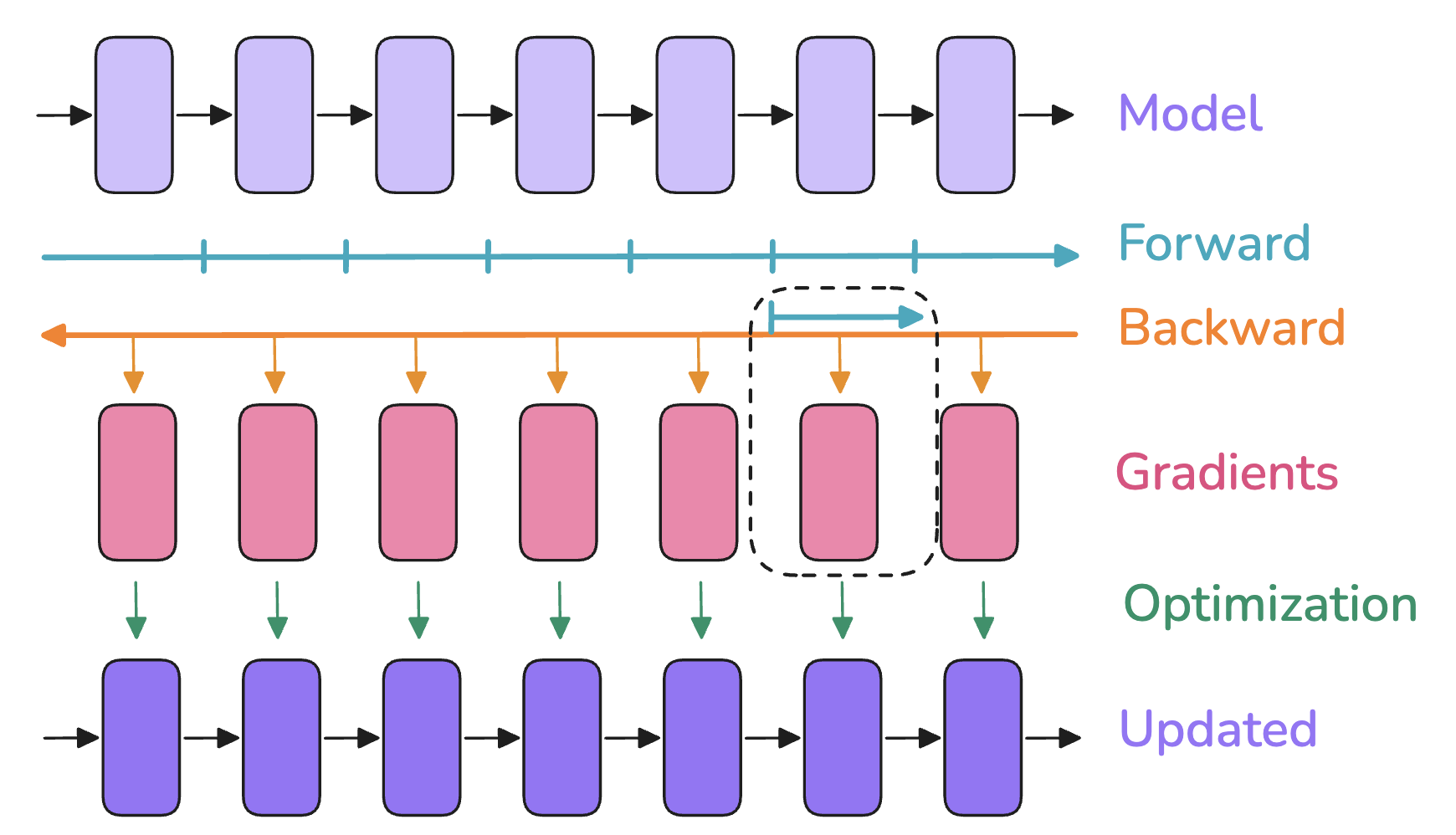
梯度累积：

图片均来自 https://huggingface.co/spaces/nanotron/ultrascale-playbook，推荐阅读