交叉熵
原文来自我的飞书:交叉熵
什么是交叉熵?
交叉熵衡量的是当我们用分布 \(Q\) 来实际编码来自分布 \(P\) 的数据时所需要的平均比特数。
其定义如下:
\[\begin{align} H(P, Q) = -\sum_{x}P(x)\log{Q(x)} \end{align}\]基本场景
什么叫做
用分布 \(Q\) 来实际编码来自分布 \(P\) 的数据时所需要的平均比特数
我们用一个实际例子来进行解释,假如我们去观测一个信息源,这个信息源会输出四种符号 \(A,B,C,D\)
其真实分布 \(P\) 满足:
-
$P(A)=0.7$
-
$P(B)=0.1$
-
$P(C)=0.1$
-
$P(D)=0.1$
而我们所做的估计分布 \(Q\) 为:
-
$Q(A)=0.25$
-
$Q(B)=0.25$
-
$Q(C)=0.25$
-
$Q(D)=0.25$
最优编码长度
根据信息论,符号的最优编码长度应该是其概率的负对数:\(-\log_2(p)\)
因此,假如我们根据真实分布 \(P\)来做最优编码的话,每个符号对应的最优编码长度为:
-
$l_A=-\log_2P(A)=0.51\text{ bit}$
-
$l_B=-\log_2P(B)=3.32\text{ bit}$
-
$l_C=-\log_2P(C)=3.32 \text{ bit}$
-
$l_D=-\log_2P(D)=3.32 \text{ bit}$
而假如我们用估计分布 \(Q\) 来做最优编码的话,每个符号对应的最优编码长度为:
-
$l_A=-\log_2P(A)=2.00\text{ bit}$
-
$l_B=-\log_2P(B)=2.00\text{ bit}$
-
$l_C=-\log_2P(C)=2.00 \text{ bit}$
-
$l_D=-\log_2P(D)=2.00 \text{ bit}$
实际编码方案
这里我们发现最优编码长度可能会是小数,在实际应用当中,会采用整数长度进行近似,比如我们可以设计如下的编码方案:
基于实际分布 \(P\) 的编码方案(用哈夫曼编码近似)
-
A: “0”(1 bit)
-
B: “10”(2 bit)
-
C: “110”(3 bit)
-
D: “111”(3 bit)
基于估计分布 \(Q\) 的编码方案(均匀分布)
-
A: “00”(2 bit)
-
B: “01”(2 bit)
-
C: “10”(2 bit)
-
D: “11”(2 bit)
计算平均编码长度
使用 P 的编码方案来编码 P 分布的数据
\[平均编码长度=P(A)×长度(A)+P(B)×长度(B)+P(C)×长度(C)+P(D)×长度(D)\] \[平均编码长度 = P(A) \times 1 + P(B) \times 2 + P(C) \times 3 + P(D) \times 3 = 1.60\]以上每个符号的长度选用的是实际的编码方案,而非最优编码。
使用 Q 的编码方案来编码 P 分布的数据
这也就是交叉熵
\[交叉熵\ H(P,Q)=\sum_{x\in\{A,B,C,D\}}P(x)×(-\log_2Q(x))\] \[平均编码长度 = P(A) \times 2 + P(B) \times 2 + P(C) \times 2 + P(D) \times 2 = 2.00\]这里的直观理解如下:
-
当使用为 \(P\) 优化的编码方案来编码 \(P\) 分布的数据时,平均每个符号需要 1.60 比特,接近于 \(P\) 的熵,是理论上的最小值
-
当使用为 \(Q\) 优化的编码方案来编码 \(P\) 分布的数据时,平均每个符号需要 2.00 比特,这个值就是交叉熵 \(H(P,Q)\)
-
这个差值 2.00 - 1.60 = 0.40 比特实际上表示的是由于使用了次优编码方案(为 Q 优化而不是为 P 优化)而导致的每个符号的额外开销,这里实际上就是 KL 散度 \(D(P\|Q)=H(P,Q)-H(P)\)
为什么最优编码长度是概率的负对数?
在讲解交叉熵中最优编码长度一节使用了一个结论:
根据信息论,符号的最优编码长度应该是其概率的负对数:\(-\log_2(p)\)
那么为什么是这样?
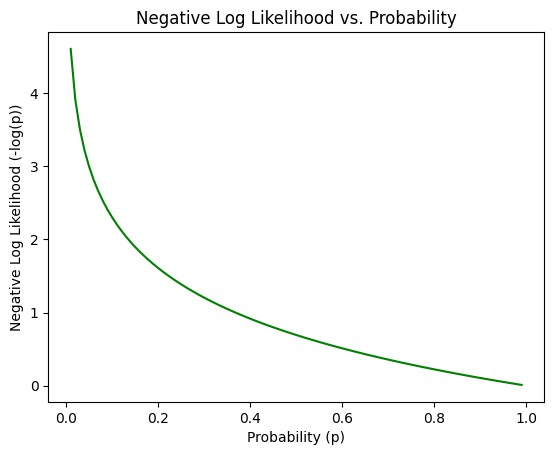
直观理解
-
稀有事件应该有更长的编码,为了减少整体的编码长度,应该给高频符号分配短编码,低频符号分配长编码
-
信息论认为,一个事件包含的信息量和不确定性有关,概率低的事件发生时,其带来的惊讶度越高,代表更多的信息量,因此需要更多的比特进行编码
数学推导
“最优编码长度等于其概率的负对数” 需要严格的数学证明,依赖于 Kraft 不等式。
Kraft 不等式
对于任意一个可以一次性解码(不需要等待更多比特来消除歧义)的前缀码(所有编码都不会是另一个编码的前缀)来说,必须满足 Kraft 不等式:
\[\begin{align} \sum_{i=1}^n2^{-l_i}\le 1 \end{align}\]其中 \(l_i\) 是第 \(i\)个符号的编码长度。这个不等式是怎么来的?从直观理解上,我们考虑每一个编码都为一个 01 序列,每一位选择 0 或 1 的概率均等为 \(\frac{1}{2}\),那么长度为 \(l_i\) 的编码,其对应的概率就是 \(2^{-l_i}\),又由于每个编码出现的事件概率是独立的,因此他们的概率和应该 \(\le 1\),即有 \(\sum_{i=1}^n2^{-l_i}\le 1\)。
最优编码的条件
有了 Kraft 不等式之后,为了满足最小化平均编码长度,我们希望
\[\begin{align} \text{minimize } l &= \sum_{i=1}^n p_i\cdot l_i\\ \text{ s.t. } &\sum_{i=1}^n2^{-l_i}\le1\notag \end{align}\]其中 \(p_i\) 表示第 \(i\)个符号出现的概率,这个明显是一个带约束的最优化问题,可以使用拉格朗日乘数法求解。
注:此处 Kraft 不等式可以推广到 McMillan 不等式,他俩的唯一区别就是 Kraft 限定了前缀码+可一次性解码两个条件,后者只限定了可一次性解码(不要求一定是前缀码)。
拉格朗日乘数法求解
\[\begin{align} L(l_1,l_2,...,l_n,\lambda)=\sum_{i=1}^np_i\cdot l_i-\lambda(\sum_{i=1}^n2^{-l_i}-1) \end{align}\]对 \(l_i\)求偏导,并设为 \(0\):
\[\begin{align} \frac{\partial L}{\partial l_i}=p_i+\lambda\cdot 2^{-l_i}\cdot \ln(2)&=0\\ 2^{-l_i}&=-\frac{p_i}{\lambda\cdot \ln(2)} \end{align}\]然后对 \(\lambda\) 求偏导,并设为 \(0\):
\[\begin{align} \sum_{i=1}^n2^{-l_i}=1 \end{align}\]联立上面两个式子,可以得到 \(2^{-l_i}=p_i\),即 \(l_i=-\log_2(p_i)\)。
交叉熵的下界是什么?
交叉熵 \(H(P,Q)\) 的下界是分布 \(P\) 本身的熵 \(H(P)\),这一点的证明需要涉及到 KL 散度。
定义回顾
熵的定义
分布 \(P\) 的熵为:
\[\begin{align} H(P)=-\sum_i p_i\log_2(p_i) \end{align}\]交叉熵的定义
分布 \(P\) 相较于分布 \(Q\) 的交叉熵定义为:
\[\begin{align} H(P,Q)=-\sum_ip_i\log_2(q_i) \end{align}\]交叉熵与 KL 散度的关系
交叉熵 减去 熵即为 KL 散度(Kullback-Leibler Divergence):
\[\begin{align} H(P,Q)=H(P)+D_{KL}(P\|Q) \end{align}\]其中 KL 散度的定义为:
\[\begin{align} D_{KL}(P\|Q)=\sum_ip_i\log_2(\frac{p_i}{q_i}) \end{align}\]交叉熵的下界
KL 散度有一个重要的性质是 \(D_{KL}(P\|Q)\ge 0\),当且仅当 \(P=Q\) 时取等号,因此有:
\[\begin{align} H(P,Q)=H(P)+D_{KL}(P\|Q)\ge H(P) \end{align}\]也就是说,交叉熵 \(H(P,Q)\) 的下界为 \(H(P)\)。
KL 散度有一个重要的性质是 \(D_{KL}(P\|Q)\ge 0\)
这个性质如何证明?可以使用对数不等式或者 Jensen 不等式,以下给出使用对数不等式的证法:
\[\begin{align} D_{KL}(P\|Q)&=\sum_i p_i\log_2(\frac{p_i}{q_i})\\ &=-\sum_i p_i\log_2(\frac{q_i}{p_i})\\ &\ge-\sum_ip_i(\frac{q_i}{p_i}-1)\quad 使用对数不等式 -\log(x)\ge x-1\\ &=-\sum_i(q_i-p_i)\\ &=-(1-1)\\ &=0 \end{align}\]这里的证明技巧是你要记得取个负号让 \(p_i\) 放到分母上,也就是公式的第二步。
此处 \(H(P,Q)\ge H(P)\) 实际上就是 Gibbs 不等式。
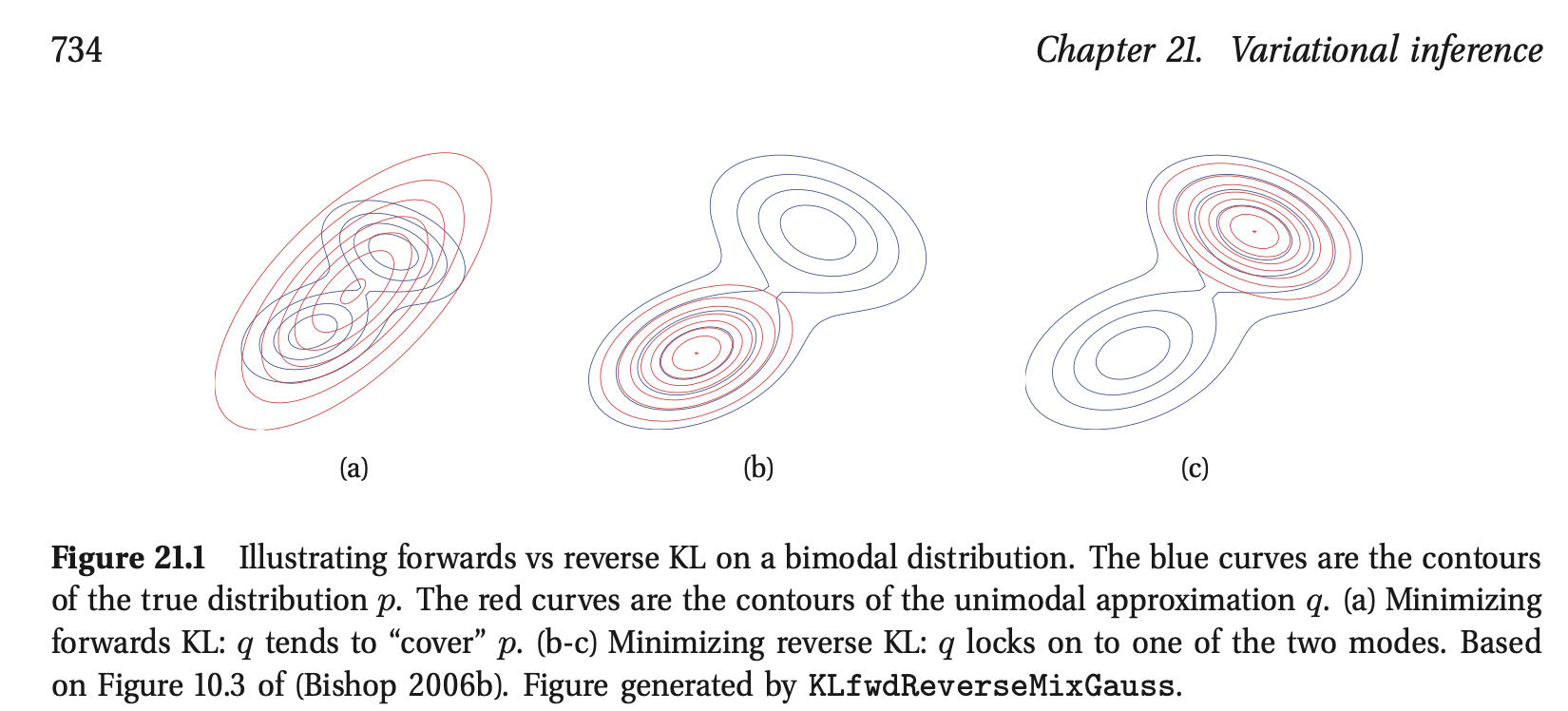
如何理解交叉熵和 KL 散度的不对称性?
我们如果仔细观察交叉熵和 KL 散度的话,会发现他们是不对称的:
\[\begin{align} H(P,Q)=-\sum_ip_i\log(q_i)&\not=-\sum_iq_i\log(p_i)=H(Q,P)\\ D_{KL}(P\|Q)=\sum_ip_i\log(\frac{p_i}{q_i})&\not=\sum_iq_i\log(\frac{q_i}{p_i})=D_{KL}(Q\|P) \end{align}\]这种不对称有其深刻含义,以下仅讨论 KL 散度的不对称性,交叉熵的不对称性是类似的。
假设 \(P\) 为实际分布,\(Q\) 为估计分布,对于最小化 \(D_{KL}(P\|Q)\) (也叫前向 KL 散度)来说,估计的分布 \(Q\) 会倾向于贴近 \(P\) 的所有高概率区域,因为假如 \(Q\) 在 \(P\) 的高概率区域分配了低概率,惩罚会很大(惩罚来源于 \(-p_i\log(\frac{p_i}{q_i})\)),而假如 \(P\) 的某些区域概率接近 \(0\),那么即使 \(Q\) 在这些区域分配了高概率,也不会产生很大的惩罚,因此这会导致“平均寻找”(mean-seeking behavior):\(Q\) 会尝试覆盖 \(P\) 的所有模式,即使这意味着 \(Q\) 必须在 \(P\) 的低概率区域也分配一些概率。
同样假设 \(P\) 为实际分布,\(Q\) 为估计分布,对于最小化 \(D_{KL}(Q\|P)\) (也叫反向 KL 散度)来说,则是关注 \(Q\)的高概率区域,假如 \(P\) 在 \(Q\) 的高概率区域分配了低概率,惩罚会很大。但是假如 \(Q\) 的在某个区域的概率接近 \(0\),那么即使 \(P\) 在这个区域有高概率,惩罚也会很小,这最终会导致“模式寻找”(mode-seek behavior):\(Q\) 只会在 \(P\) 的某些高概率区域分配高概率,不保证覆盖到 \(P\) 的所有高概率区域。
下图来自 Machine Learning: A Probabilistic Perspective 第 21.2.2 节